
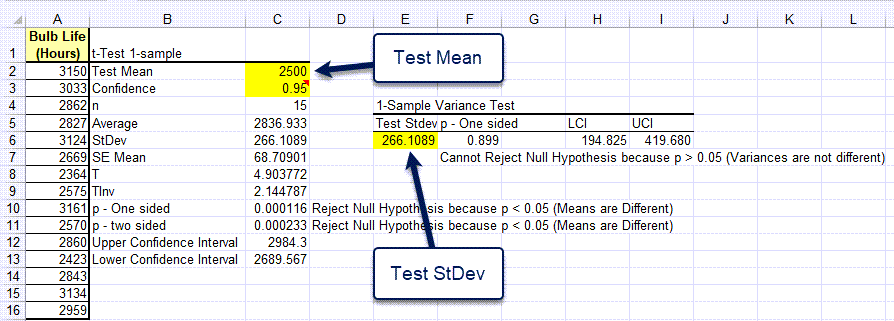
If we have fewer than ?30? samples, then the original distribution needs to be normal.īut assuming that we know the original distribution is normal (in which case sample size doesn’t matter), or that we have at least ?30? samples (in which case the original distribution will be normalized by the CLT), and if population standard deviation ?\sigma? is known, then the value of the test statistic is Remember that we need at least ?30? samples in order for the Central Limit Theorem to apply and normalize the distribution. The formula we’ll use to calculate the test statistic depends on the information we have and the size of our sample. The next step is always to calculate the test statistic, and then determine whether that value lies inside or outside the region of rejection. We can also find the boundary or boundaries of the region region based on the alpha value and which test type we’re using.
#ONE TAIL HYPOTHESIS TEST CALCULATOR HOW TO#
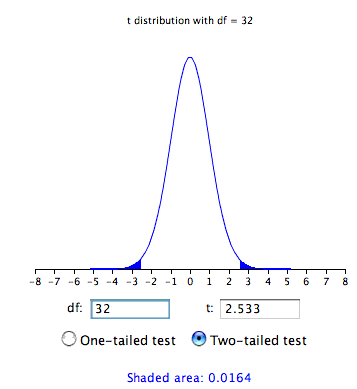
Which means the difference could by in either direction (less than or greater than), which means we’ll have two rejection regions in the distribution.įor a lower-tail test, you’ll find the boundary of the rejection region at a ?z?-score for ?0.1000?.Ĭalculating the test statistic when standard deviation is known and unknown, and when sample size is large and smallĪt this point, we know how to write the hypothesis statements, determine the alpha level we want to use, and set up a one- or two-tailed test based on the hypothesis statements. We’re not saying that one value is greater or less than the other, we’re just saying that they’re different. When we state in the null hypothesis that the population mean or population proportion is equal to some value, and then state with the alternative hypothesis that the mean or proportion is not equal to that value, we’re not predicting any direction between the variables. Here’s the way to understand one- and two-tailed tests. ?H_0? with a ?\ge? sign and ?H_a? with a ?, or ?\geq? and ? 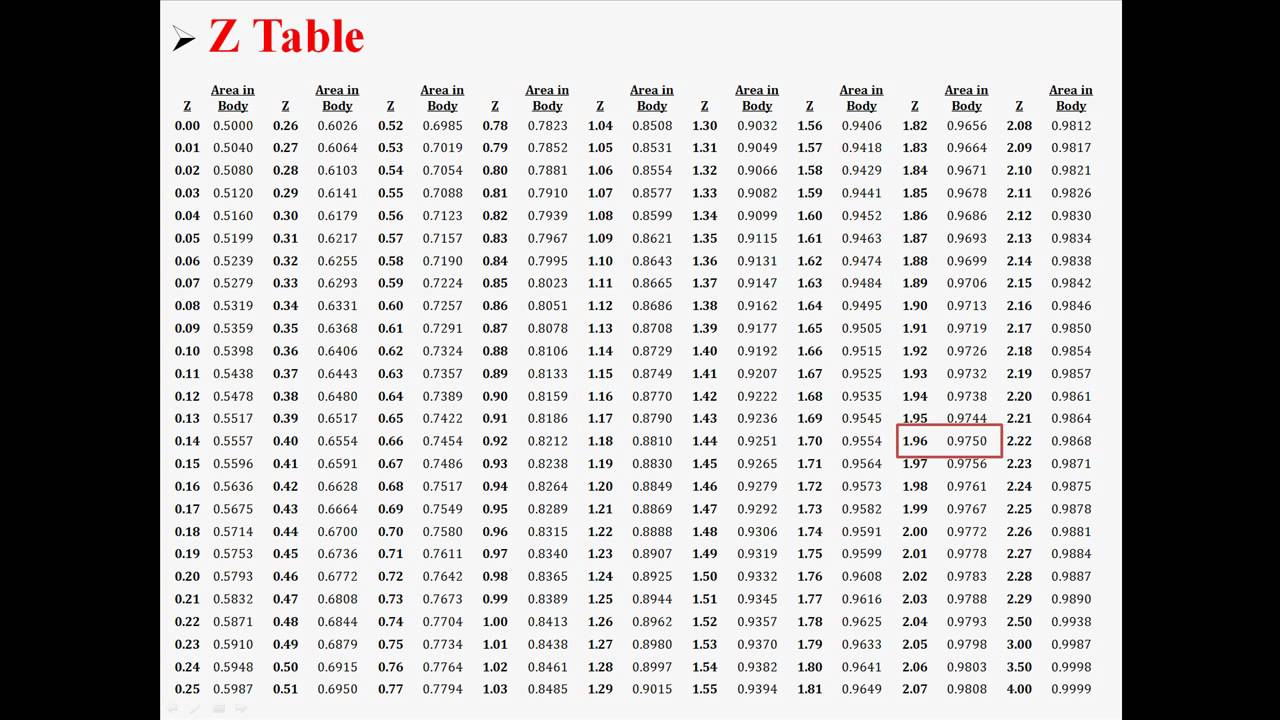
?H_0? with a ?\le? sign and ?H_a? with a ?>? sign ?H_0? with an ?=? sign and ?H_a? with a ?\ne? sign We’ve already learned that, for both means and proportions, we can write the null and alternative hypothesis statements in three ways: So let’s define one- and two-tailed tests, and start over with the hypothesis statements to show when we’ll use each test type. Whether we run a one- or two-tail test is dictated by the hypothesis statements we wrote in the first step. But any test statistic we calculate will depend on whether we’re running a two-tail test or a one-tail test. We’ve already covered the first two steps, and now we want to talk about how to calculate the test statistic.


 0 kommentar(er)
0 kommentar(er)
